Imagine that we have a robot and we want the robot to learn the most efficient way to exit from a house.
So we place the robot in a random room and the robot tries to exit from the house.
The robot learns from the successes and the failures, and starts improving. In a few tries the robot knows
the most efficient way to exit from the house
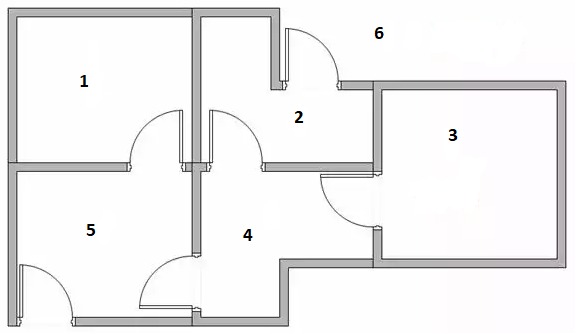
If the robot starts in the room 1 or in the room 3, there is nothing to choose. From the room 1 he can only goes to room 5.
From the room 3 he can only go to room 4.
If he is in the room 2, then he has two options, to exit from the house (he does not know it is the exit but he will get rewarded)
or he may go to room 4.
A similar situation happens in the room 5. he may exit from the house (and get rewarded) or he may go to room 4 or room 1.
When the robot is in the room 4 he has two alternatives to exit: going through room 5 or going through room 2. Both ways
will take him out of the house in the same amount of steps.
When the robot exits the house, he gets a positive reinforcement (the State's nScore increases in 0.1). When he fails, he gets
a negative reinforcement (the state's nScore decreases in 0.1). After a few tries, the robot learns the right way.
qlearning.prg
- Code: Select all Expand view RUN
- #include "FiveWin.ch"
static aStates
//----------------------------------------------------------------------------//
function Main()
local n
aStates = InitStates()
for n = 1 to 10
? "Number of steps to exit", SolveIt()
next
XBrowse( aStates )
return nil
//----------------------------------------------------------------------------//
function SolveIt()
local oState, nSteps := 0
oState = aStates[ hb_RandomInt( 1, Len( aStates ) - 1 ) ]
while ! oState == ATail( aStates )
XBrowse( oState:aOptions, "Options for room: " + AllTrim( Str( oState:nId ) ) )
oState = oState:NextState()
nSteps++
end
return nSteps
//----------------------------------------------------------------------------//
function InitStates()
local aStates := Array( 6 )
AEval( aStates, { | o, n | aStates[ n ] := TState():New( n ) } )
aStates[ 1 ]:AddOption( aStates[ 5 ] )
aStates[ 2 ]:AddOption( aStates[ 4 ] )
aStates[ 2 ]:AddOption( aStates[ 6 ] )
aStates[ 3 ]:AddOption( aStates[ 4 ] )
aStates[ 4 ]:AddOption( aStates[ 2 ] )
aStates[ 4 ]:AddOption( aStates[ 3 ] )
aStates[ 4 ]:AddOption( aStates[ 5 ] )
aStates[ 5 ]:AddOption( aStates[ 1 ] )
aStates[ 5 ]:AddOption( aStates[ 4 ] )
aStates[ 5 ]:AddOption( aStates[ 6 ] )
aStates[ 6 ]:AddOption( aStates[ 2 ] )
aStates[ 6 ]:AddOption( aStates[ 5 ] )
return aStates
//----------------------------------------------------------------------------//
CLASS TState
DATA nId
DATA aOptions INIT {}
DATA nScore INIT 0
METHOD New( nId ) INLINE ::nId := nId, Self
METHOD AddOption( oState ) INLINE AAdd( ::aOptions, oState )
METHOD NextState()
ENDCLASS
//----------------------------------------------------------------------------//
METHOD NextState() CLASS TState
local n, nMax := 0, oState, aOptions
if Len( ::aOptions ) == 1
oState = ::aOptions[ 1 ]
else
aOptions = AShuffle( AClone( ::aOptions ) )
for n = 1 to Len( aOptions )
if aOptions[ n ]:nScore >= nMax
nMax = aOptions[ n ]:nScore
oState = aOptions[ n ]
endif
next
endif
if oState:nId == 6
::nScore += .1
else
::nScore -= .1
endif
return oState
//----------------------------------------------------------------------------//
function AShuffle( aArray )
return ASort( aArray,,, { || HB_RandomInt( 1, 1000 ) < HB_RandomInt( 1, 1000 ) } )
//----------------------------------------------------------------------------//
After a few tries the robot starts learning, we can check it reviewing the different state's rewards:
When the robot is in room 5, he has three alternatives: room 1 (reward value is -0.3), room 4 (reward value is -0.3) and option 6 (reward zero)
so he takes the highest value and knows that option 6 is the right one
