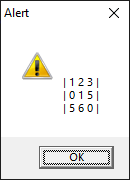
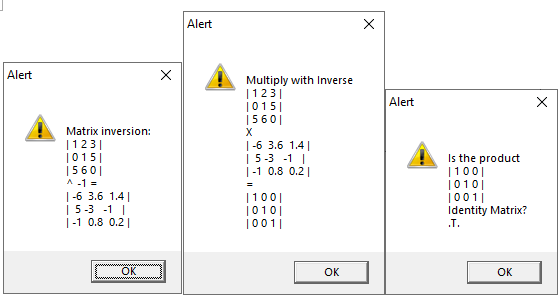
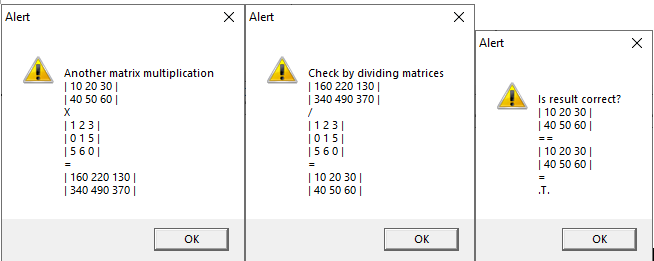
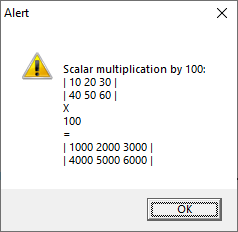
A library of C functions is provided to build highly efficient C level programs. These functions are independent of FW_Matrix class.
In this library, matrix is stored in the following structure:
Code: Select all | Expand
typedef struct _MATRIX
{
int rows;
int cols;
int len;
int xlen;
double * array;
} MATRIX, * PMATRIX;
Harbour level functions to access the C level functions:
Code: Select all | Expand
MATRIX_CREATE( aArray ) --> Pointer to Matrix structure using aArray
MATRIX_IDENTITY( nSize ) --> pIdentityMatrix
MATRIX_RANDOM ( nRows, nCols, nMin = -1.0, nMax = 1.0, lIntegers ) --> pRandomMatrix
MATRIX_RELEASE( pMatrix )
MATRIX_TRANSPOSE( pMatrix ) --> pTransposedMatrix
MATRIX_VAL( pMatrix, nRow, nCol ) --> Value
MATRIX_ROW( pMatrix, nRow ) --> aRow
MATRIX_ARRAY( pMatrix ) --> aMatrix
MATRIX_INVERT( pMatrix ) --> Inverse of pMatrix
MATRIX_REFLECT( pMatrix ) --> Transposes the same Square Matrix
MATRIX_CALC( pmatrix1, cOp, double/pmatrix2, [lReverse], [presultmatrix] ) --> pResultMatrix
MATRIX_MMULT( pmatrix1, pmatrix2 ) --> pProductMatrix
MATRIX_DETERMINANT( pMatrix ) --> determinant
MATRIX_SUMOFROWS( matrix, [result] ) --> result
C functions that can be used in an application program written in C.
Code: Select all | Expand
double calc( double x, char cOp, double y, HB_BOOL inverse );
PMATRIX matrix_new( int iRows, int iCols );
void matrix_release( MATRIX * matrix );
PMATRIX matrix_check( PMATRIX matrix, int iRows, int iCols );
PMATRIX matrix_clone( MATRIX * matrix );
void matrix_copyfrom( PMATRIX dst, PMATRIX src );
PMATRIX matrix_identity( int iSize );
PMATRIX matrix_random( int iRows, int iCols, double dMin, double dMax, HB_BOOL bInteger );
PMATRIX matrix_transpose( PMATRIX matrix, PMATRIX result );
PMATRIX matrix_scalar_calc( PMATRIX m1, char cOp, double operand, HB_BOOL inverse, PMATRIX result );
PMATRIX matrix_sigmoid( PMATRIX matrix, PMATRIX result );
PMATRIX matrix_sigmoid_derivative( PMATRIX matrix, PMATRIX result );
PMATRIX matrix_linear_calc( PMATRIX m1, char cOp, PMATRIX m2, PMATRIX result );
PMATRIX matrix_sumofrows( PMATRIX matrix, PMATRIX result );
PMATRIX matrix_mmult( PMATRIX m1, PMATRIX m2, PMATRIX result );
double array_determinant( double * array, int iSize );
double matrix_determinant( PMATRIX matrix );
PMATRIX matrix_invert( PMATRIX matrix );
In the above functions, if the parameter PMATRIX result is NULL, a new matrix of the required size is created and returned. This needs to be released using matrix_release(). If result is a valid matrix pointer, then this matrix is used to fill the result and returned, after resizing if necessary. This avoids the overhead of creating a new matrix and releasing it.
Normally, FW_Matrix class should be enough for most applications. Where large computations are to be performed in large loops writing the code in C using these C functions improves the execution speed considerably.
Example:
This code written using FW_Matrix() is taking 3.0 to 4.0 seconds for executing 10,000 times.
Code: Select all | Expand
for i := 1 to 10000
// Forward Propagation
hidden_layer_activation := inputs * hidden_weights
hidden_layer_activation += hidden_bias
hidden_layer_output := hidden_layer_activation:Sigmoid()
output_layer_activation := hidden_layer_output * output_weights
output_layer_activation += output_bias
predicted_output := output_layer_activation:Sigmoid()
// Backpropagation
error := expected_output - predicted_output
d_predicted_output := error:Linear() * predicted_output:sigmoid_derivative()
error_hidden_layer := d_predicted_output * output_weights:Transpose()
d_hidden_layer := error_hidden_layer:Linear() * hidden_layer_output:sigmoid_derivative()
// Updating Weights and Biases
output_weights += ( hidden_layer_output:Transpose() * d_predicted_output ) * lr
output_bias += ( d_predicted_output:SumOfRows() * lr )
hidden_weights += ( inputs:Transpose() * d_hidden_layer ) * lr
hidden_bias += ( d_hidden_layer:SumOfRows() * lr )
next
When the same logic is translated using the above C functions as below, the loop is executed in about 0.01 second.
Code: Select all | Expand
#pragma BEGINDUMP
#include <hbapi.h>
#include "fwmatrix.h"
HB_FUNC( TRAIN )
{
PMATRIX inputs42 = hb_parptr( 1 );
PMATRIX expected_output41 = hb_parptr( 2 );
PMATRIX hidden_weights22 = hb_parptr( 3 );
PMATRIX hidden_bias12 = hb_parptr( 4 );
PMATRIX output_weights21 = hb_parptr( 5 );
PMATRIX output_bias11 = hb_parptr( 6 );
double lr = 0.1;
int i;
PMATRIX hidden_layer_activation42 = matrix_new( 4, 2 );
PMATRIX hidden_layer_output42 = matrix_new( 4, 2 );
PMATRIX hidden_layer_output_der42 = matrix_new( 4, 2 );
PMATRIX hidden_layer_output24 = matrix_new( 2, 4 );
PMATRIX output_layer_activation41 = matrix_new( 4, 1 );
PMATRIX predicted_output41 = matrix_new( 4, 1 );
PMATRIX error41 = matrix_new( 4, 1 );
PMATRIX predicted_output_der41 = matrix_new( 4, 1 );
PMATRIX d_predicted_output41 = matrix_new( 4, 1 );
PMATRIX d_predicted_output_sum11 = matrix_new( 1, 1 );
PMATRIX output_weights12 = matrix_new( 1, 2 );
PMATRIX error_hidden_layer42 = matrix_new( 4, 2 );
PMATRIX d_hidden_layer42 = matrix_new( 4, 2 );
PMATRIX inputs24 = matrix_new( 2, 4 );
PMATRIX tmp21 = matrix_new( 2, 1 );
PMATRIX tmp22 = matrix_new( 2, 2 );
PMATRIX tmp12 = matrix_new( 1, 2 );
for ( i = 0; i < 10000; i++ )
{
int p;
// Forward Propagation
matrix_mmult( inputs42, hidden_weights22, hidden_layer_activation42 );
matrix_linear_calc( hidden_layer_activation42, '+', hidden_bias12, hidden_layer_activation42 );
matrix_sigmoid( hidden_layer_activation42, hidden_layer_output42 );
matrix_mmult( hidden_layer_output42, output_weights21, output_layer_activation41 );
matrix_linear_calc( output_layer_activation41, '+',output_bias11, output_layer_activation41 );
matrix_sigmoid( output_layer_activation41, predicted_output41 );
// Backpropagation
matrix_linear_calc( expected_output41, '-', predicted_output41, error41 );
matrix_sigmoid_derivative( predicted_output41, predicted_output_der41 );
matrix_linear_calc( error41, '*', predicted_output_der41, d_predicted_output41 );
matrix_transpose( output_weights21, output_weights12 );
matrix_mmult( d_predicted_output41, output_weights12, error_hidden_layer42 );
matrix_sigmoid_derivative( hidden_layer_output42, hidden_layer_output_der42 );
matrix_linear_calc( error_hidden_layer42, '*', hidden_layer_output_der42, d_hidden_layer42 );
// Updating Weights and Biases
// update output_weights21
matrix_transpose( hidden_layer_output42, hidden_layer_output24 );
matrix_mmult( hidden_layer_output24, d_predicted_output41, tmp21 );
for ( p = 0; p < tmp21->len; p++ ) { tmp21->array[ p ] *= lr; }
matrix_linear_calc( output_weights21, '+', tmp21, output_weights21 );
//
// update output_bias11
matrix_sumofrows( d_predicted_output41, d_predicted_output_sum11 );
for ( p = 0; p < d_predicted_output_sum11->len; p++ ) { d_predicted_output_sum11->array[ p ] *= lr; }
matrix_linear_calc( output_bias11, '+', d_predicted_output_sum11, output_bias11 );
// update hidden_weights22
matrix_transpose( inputs42, inputs24 );
matrix_mmult( inputs24, d_hidden_layer42, tmp22 );
for ( p = 0; p < tmp22->len; p++ ) { tmp22->array[ p ] *= lr; }
matrix_linear_calc( hidden_weights22, '+', tmp22, hidden_weights22 );
// update hidden_bias12
matrix_sumofrows( d_hidden_layer42, tmp12 );
for ( p = 0; p < tmp12->len; p++ ) { tmp12->array[ p ] *= lr; }
matrix_linear_calc( hidden_bias12, '+', tmp12, hidden_bias12 );
}
hb_retptr( predicted_output41 );
matrix_release( hidden_layer_activation42 ) ;
matrix_release( hidden_layer_output42 ) ;
matrix_release( hidden_layer_output_der42 ) ;
matrix_release( hidden_layer_output24 ) ;
matrix_release( output_layer_activation41 ) ;
matrix_release( error41 ) ;
matrix_release( predicted_output_der41 ) ;
matrix_release( d_predicted_output41 ) ;
matrix_release( d_predicted_output_sum11 ) ;
matrix_release( output_weights12 ) ;
matrix_release( error_hidden_layer42 ) ;
matrix_release( d_hidden_layer42 ) ;
matrix_release( inputs24 ) ;
matrix_release( tmp21 ) ;
matrix_release( tmp22 ) ;
matrix_release( tmp12 ) ;
}
#pragma ENDDUMP
Next release of FWH provides samples nn1.prg, nn2.prg, nn3.prg, nn4.prg, nn4c.prg and matrix01.prg