Hola a todos...
Necesito armar un algoritmo que me devuelva todas las combinaciones posibles de una serie de letras formando combinaciones mayores o iguales a 3 caracteres.
Ejemplo tomando la palabra "ESTEBAN"
Obtener como resultado:
EST
ESTE
ESTEB
ESTEBAN
SET
SETB
SETBA
SETBAN
Etc, etc etc...
A alguien se le ocurre como encarar este algoritmo?
Desde ya muchas gracias.
Saludos,
Combinaciones de letras
13 posts • Page 1 of 1
Combinaciones de letras
Ojeda Esteban Eduardo.
Buenos Aires - Argentina.
FWH - PellesC - DBF/CDX - ADS - Gloriosos .Bat - MySql - C# .net - FastReport
Skype: jreduojeda
Buenos Aires - Argentina.
FWH - PellesC - DBF/CDX - ADS - Gloriosos .Bat - MySql - C# .net - FastReport
Skype: jreduojeda
-

jrestojeda - Posts: 601
- Joined: Wed Jul 04, 2007 3:51 pm
- Location: Buenos Aires - Argentina
Re: Combinaciones de letras
Estimado Esteban,
Un primer intento:
Puedes probarlo desde aqui: copia el código y selecciona Run - Execute en el menu
https://www.fivetechsoft.com/counter/modpro.php
Un primer intento:
- Code: Select all Expand view RUN
- function Main()
local cWord := "ESTEBAN", cChar, cResult, n
local aResults := {}
for each cChar in cWord
for n = 3 to Len( cWord )
if Len( cResult := SubStr( cWord, cChar:__enumIndex(), n ) ) >= 3
if AScan( aResults, cResult ) == 0
AAdd( aResults, cResult )
endif
endif
next
next
? ASort( aResults )
return nil
Puedes probarlo desde aqui: copia el código y selecciona Run - Execute en el menu
https://www.fivetechsoft.com/counter/modpro.php
-

Antonio Linares - Site Admin
- Posts: 42107
- Joined: Thu Oct 06, 2005 5:47 pm
- Location: Spain
Re: Combinaciones de letras
Le acabo de pedir a la inteligencia artificial de chatGPT https://chat.openai.com/chat lo siguiente:
y ha respondido esto
Y además te explica lo que ha hecho:
Estoy viendo si genera código Harbour también
write a C program that given a word will provide all the three letters or more combinations
y ha respondido esto
- Code: Select all Expand view RUN
- #include <stdio.h>
#include <string.h>
// Function to print all possible combinations of three or more letters
// in the given word
void print_combinations(char *word)
{
int len = strlen(word);
// Loop over all possible combinations of three or more letters
// in the given word
for (int i = 0; i < len; i++)
{
for (int j = i + 1; j < len; j++)
{
for (int k = j + 1; k < len; k++)
{
printf("%c%c%c\n", word[i], word[j], word[k]);
}
}
}
}
int main()
{
char word[100]; // Store the word
printf("Enter a word: ");
scanf("%s", word);
printf("All possible combinations of three or more letters in '%s' are:\n", word);
// Call the function to print all combinations
print_combinations(word);
return 0;
}
Y además te explica lo que ha hecho:
This program uses a nested loop to generate all possible combinations of three or more letters in the given word. The outer two loops iterate over all pairs of letters in the word, and the inner loop iterates over all remaining letters in the word to generate a combination of three letters. The combination is then printed on a new line.
Estoy viendo si genera código Harbour también
-

Antonio Linares - Site Admin
- Posts: 42107
- Joined: Thu Oct 06, 2005 5:47 pm
- Location: Spain
Re: Combinaciones de letras
Increible, sabe programar en Harbour !!! 
Y la explicación
escribe un programa en Harbour que dada una palabra genere todas las posibles combinaciones de 3 o más letras que haya en la palabra
- Code: Select all Expand view RUN
- // Función para imprimir todas las posibles combinaciones de 3 o más letras
// en la palabra dada
PROCEDURE print_combinations(cWord)
LOCAL cCombination[4], i, j, k, nLen
// Obtener la longitud de la palabra
nLen := LEN(cWord)
// Recorrer todas las posibles combinaciones de 3 o más letras
// en la palabra dada
FOR i := 1 TO nLen
FOR j := i + 1 TO nLen
FOR k := j + 1 TO nLen
// Generar la combinación de 3 letras
cCombination := SUBSTR(cWord, i, 1) + SUBSTR(cWord, j, 1) + SUBSTR(cWord, k, 1)
// Imprimir la combinación
? cCombination
NEXT
NEXT
NEXT
RETURN NIL
// Programa principal
PROCEDURE Main()
LOCAL cWord[100] // Almacenar la palabra
// Pedir la palabra al usuario
INPUT "Ingrese una palabra: ", cWord
// Imprimir el título
? "Todas las posibles combinaciones de 3 o más letras en '", cWord, "' son:"
// Llamar a la función para imprimir las combinaciones
print_combinations(cWord)
RETURN
Y la explicación
Este programa utiliza un bucle anidado para generar todas las posibles combinaciones de 3 o más letras en la palabra dada. Los dos primeros bucles recorren todos los pares de letras en la palabra, y el bucle interno recorre todas las letras restantes en la palabra para generar una combinación de 3 letras. Luego se imprime la combinación en una nueva línea.
-

Antonio Linares - Site Admin
- Posts: 42107
- Joined: Thu Oct 06, 2005 5:47 pm
- Location: Spain
Re: Combinaciones de letras
Estoy impresionado 
He probado el código y fallaba asi que le he dicho que lo corrigiese, en dos intentos ha corregido el código y ahora funciona bien. Lo cual quiere decir que aprende y es capaz de corregir sus propios fallos !!!
Y la explicación de lo que ha hecho:
He probado el código y fallaba asi que le he dicho que lo corrigiese, en dos intentos ha corregido el código y ahora funciona bien. Lo cual quiere decir que aprende y es capaz de corregir sus propios fallos !!!
sigue generando palabras de solo 3 letras. Por favor corrigelo
Aquí está una versión actualizada del programa en Harbour que genera todas las posibles combinaciones de 3 o más letras en una palabra dada:
- Code: Select all Expand view RUN
- // Función para imprimir todas las posibles combinaciones de 3 o más letras
// en la palabra dada
PROCEDURE print_combinations(cWord)
LOCAL cCombination[100], i, j, k, l, nLen
// Obtener la longitud de la palabra
nLen := LEN(cWord)
// Recorrer todas las posibles combinaciones de 3 o más letras
// en la palabra dada
FOR i := 1 TO nLen
FOR j := i + 1 TO nLen
FOR k := j + 1 TO nLen
// Generar la combinación de 3 letras
cCombination := SUBSTR(cWord, i, 1) + SUBSTR(cWord, j, 1) + SUBSTR(cWord, k, 1)
// Añadir más letras a la combinación si es posible
FOR l := k + 1 TO nLen
cCombination += SUBSTR(cWord, l, 1)
NEXT
// Imprimir la combinación
? cCombination
NEXT
NEXT
NEXT
RETURN NIL
// Programa principal
PROCEDURE Main()
LOCAL cWord[100] // Almacenar la palabra
// Pedir la palabra al usuario
// INPUT "Ingrese una palabra: ", cWord
cWord = "ESTEBAN"
// Imprimir el título
? "Todas las posibles combinaciones de 3 o más letras en '", cWord, "' son:"
// Llamar a la función para imprimir las combinaciones
print_combinations(cWord)
RETURN
ETEBAN
ETBAN
ETAN
ETN
EEBAN
EEAN
EEN
EBAN
EBN
EAN
STEBAN
STBAN
STAN
STN
SEBAN
SEAN
SEN
SBAN
SBN
SAN
TEBAN
TEAN
TEN
TBAN
TBN
TAN
EBAN
EBN
EAN
BAN
Y la explicación de lo que ha hecho:
En esta versión del programa, se agregó un cuarto bucle que recorre todas las letras restantes después de las primeras tres letras y las añade a la combinación si es posible. De esta manera, se pueden generar combinaciones de cualquier longitud mayor o igual a 3
-

Antonio Linares - Site Admin
- Posts: 42107
- Joined: Thu Oct 06, 2005 5:47 pm
- Location: Spain
Re: Combinaciones de letras
Espectacular.
Así a simple vista parece algo sencillo pero se me hizo una laguna y no sabía por donde encarar el problema.
Muy bueno Antonio.
Muchas gracias.
Así a simple vista parece algo sencillo pero se me hizo una laguna y no sabía por donde encarar el problema.
Muy bueno Antonio.
Muchas gracias.
Ojeda Esteban Eduardo.
Buenos Aires - Argentina.
FWH - PellesC - DBF/CDX - ADS - Gloriosos .Bat - MySql - C# .net - FastReport
Skype: jreduojeda
Buenos Aires - Argentina.
FWH - PellesC - DBF/CDX - ADS - Gloriosos .Bat - MySql - C# .net - FastReport
Skype: jreduojeda
-

jrestojeda - Posts: 601
- Joined: Wed Jul 04, 2007 3:51 pm
- Location: Buenos Aires - Argentina
Re: Combinaciones de letras
Antonio...
Estuve analizando las respuestas, y creo que el resultado no es el esperado.
Es decir, faltan combinaciones.
Por ej no veo que me devuelva las combinaciones que comiencen con "N".
Estuve analizando las respuestas, y creo que el resultado no es el esperado.
Es decir, faltan combinaciones.
Por ej no veo que me devuelva las combinaciones que comiencen con "N".
Ojeda Esteban Eduardo.
Buenos Aires - Argentina.
FWH - PellesC - DBF/CDX - ADS - Gloriosos .Bat - MySql - C# .net - FastReport
Skype: jreduojeda
Buenos Aires - Argentina.
FWH - PellesC - DBF/CDX - ADS - Gloriosos .Bat - MySql - C# .net - FastReport
Skype: jreduojeda
-

jrestojeda - Posts: 601
- Joined: Wed Jul 04, 2007 3:51 pm
- Location: Buenos Aires - Argentina
Re: Combinaciones de letras
Prueba con chatGPT y ve dandole indicaciones hasta que funcione de forma deseada 
-

Antonio Linares - Site Admin
- Posts: 42107
- Joined: Thu Oct 06, 2005 5:47 pm
- Location: Spain
Re: Combinaciones de letras
Muchas gracias Antonio.
Saludos,
Saludos,
Ojeda Esteban Eduardo.
Buenos Aires - Argentina.
FWH - PellesC - DBF/CDX - ADS - Gloriosos .Bat - MySql - C# .net - FastReport
Skype: jreduojeda
Buenos Aires - Argentina.
FWH - PellesC - DBF/CDX - ADS - Gloriosos .Bat - MySql - C# .net - FastReport
Skype: jreduojeda
-

jrestojeda - Posts: 601
- Joined: Wed Jul 04, 2007 3:51 pm
- Location: Buenos Aires - Argentina
Re: Combinaciones de letras
Hola, eso se llama combinatoria en matemáticas y hay fórmulas para resolverlo.
Saludos
Saludos
- horacio
- Posts: 1363
- Joined: Wed Jun 21, 2006 12:39 am
- Location: Capital Federal Argentina
Re: Combinaciones de letras
Entiendo que las formulas de combinatorias nos dicen cuantas combinaciones tenemos.
Pero yo necesito saber cuales son esas combinaciones.
Pero yo necesito saber cuales son esas combinaciones.
Ojeda Esteban Eduardo.
Buenos Aires - Argentina.
FWH - PellesC - DBF/CDX - ADS - Gloriosos .Bat - MySql - C# .net - FastReport
Skype: jreduojeda
Buenos Aires - Argentina.
FWH - PellesC - DBF/CDX - ADS - Gloriosos .Bat - MySql - C# .net - FastReport
Skype: jreduojeda
-

jrestojeda - Posts: 601
- Joined: Wed Jul 04, 2007 3:51 pm
- Location: Buenos Aires - Argentina
Re: Combinaciones de letras
Creo que puede ser algo asi:
- Code: Select all Expand view RUN
// Función para imprimir todas las posibles combinaciones de 3 o más letras
// en la palabra dada
PROCEDURE Main()
LOCAL cCombination[100], i, j, k, l, nLen, cWord := "ESTEBAN", aArray := {}
// Obtener la longitud de la palabra
nLen := LEN(cWord)
// Recorrer todas las posibles combinaciones de 3 o más letras
// en la palabra dada
FOR i := 1 TO nLen
FOR j := 1 TO nLen
IF j <> i
FOR k := 1 TO nLen
IF k <> j .and. k <> i
// Generar la combinación de 3 letras
cCombination := SUBSTR(cWord, i, 1) + SUBSTR(cWord, j, 1) + SUBSTR(cWord, k, 1)
IF ASCAN(aArray,cCombination) == 0
AADD(aArray,cCombination)
ENDIF
// Añadir más letras a la combinación si es posible
FOR l := 1 TO nLen
if l <> k .and. l <> i .and. l <> j
cCombination += SUBSTR(cWord, l, 1)
IF ASCAN(aArray,cCombination) == 0
AADD(aArray,cCombination)
ENDIF
endif
NEXT
endif
NEXT
ENDIF
NEXT
NEXT
xbrowse(aArray)
RETURN NIL
-

cmsoft - Posts: 1290
- Joined: Wed Nov 16, 2005 9:14 pm
- Location: Mercedes - Bs As. Argentina
Re: Combinaciones de letras
jrestojeda wrote:Hola a todos...
Necesito armar un algoritmo que me devuelva todas las combinaciones posibles de una serie de letras formando combinaciones mayores o iguales a 3 caracteres.
Ejemplo tomando la palabra "ESTEBAN"
Obtener como resultado:
EST
ESTE
ESTEB
ESTEBAN
SET
SETB
SETBA
SETBAN
Etc, etc etc...
A alguien se le ocurre como encarar este algoritmo?
Desde ya muchas gracias.
Saludos,
From your posting, what you are looking for are not just combinations but all permutations of
( 3 of 7 ) + ( 4 of 7 ) + ( 5 of 7 ) + ( 6 of 7 ) + ( 7 of 7 ) characters.
If each character in the source string is unique, we get a total of 13,650 permutations (from 99 combinations).
Forumla:
- Code: Select all Expand view RUN
fact(7)/fact(4) + fact(7)/fact(3) + fact(7)/fact(2) + fact(7) + fact(7) // --> 13,650
FACT(n) is a function in CTLIB, which gives factorial of n.
However the alphabet "E" is repeated twice resulting in some duplicate results. Ignoring such duplicates, we get 95 combinations finally resulting in 8,553 total permutations.
Program to generate all unique combinations and permutations:
- Code: Select all Expand view RUN
- #include "fivewin.ch"
static aPrm := {}
static aCmb := {}
static aResult := {}
function Main()
local cSrc := "ESTEBAN"
local n
for n := 3 to Len( cSrc )
Combinations( n, "", cSrc )
next
for n := 1 to Len( aCmb )
aPrm := {}
Permutations( "", aCmb[ n ] )
AMERGE( aResult, aPrm )
next
XBROWSER aCmb SHOW RECID TITLE "COMBINATIONS"
XBROWSER aResult SHOW RECID TITLE "PERMUTATIONS"
// ? fact(7)/fact(4) + fact(7)/fact(3) + fact(7)/fact(2) + fact(7) + fact(7)
return nil
function Combinations( r, cCmb, cSrc )
local nLen := Len( cSrc )
local n
if r == 0
if AScan( aCmb, cCmb ) == 0
AAdd( aCmb, cCmb )
endif
else
for n := 1 to ( nLen - r + 1 )
Combinations( r - 1, cCmb + SUBSTR( cSrc, n, 1 ), SUBSTR( cSrc, n + 1 ) )
next
endif
return nil
function Permutations( cLeft, cRight )
local nLen := Len( cRight )
local n
if nLen == 0
if AScan( aPrm, cLeft ) == 0
AAdd( aPrm, cLeft )
endif
else
for n := 1 to nLen
Permutations( cLeft + SUBSTR( cRight, n, 1 ), ;
Left( cRight, n - 1 ) + SubStr( cRight, n + 1 ) )
next
endif
return nil
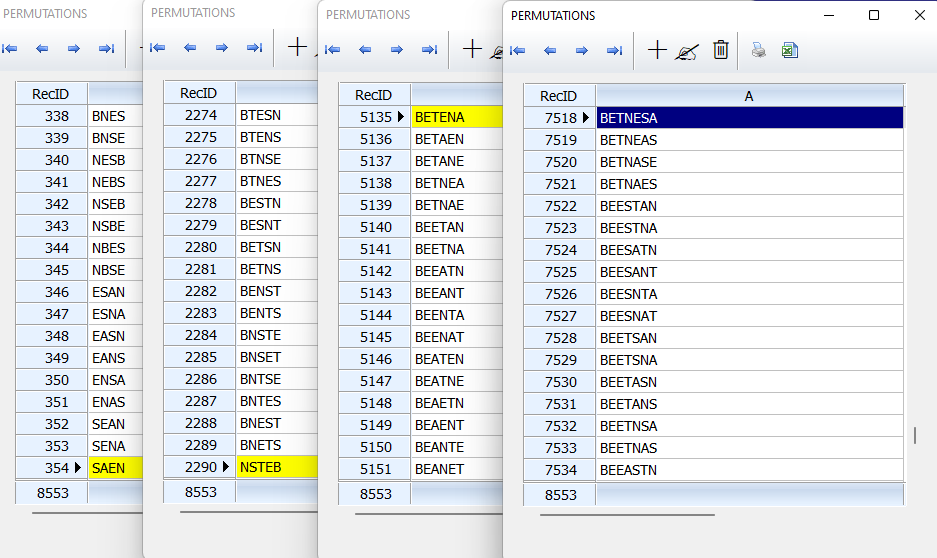
So far, this is of mathematical interest.
But I am wondering what can be the practical use of this huge result-set.
Formulae of interest:
Total permutations of r out of n = n! / ( n - r )!
Total combinations of r out of n = n! / ( r! * ( n - r )! )
where n! is Factorial( n )
Regards
G. N. Rao.
Hyderabad, India
G. N. Rao.
Hyderabad, India
-

nageswaragunupudi - Posts: 10646
- Joined: Sun Nov 19, 2006 5:22 am
- Location: India
13 posts • Page 1 of 1
Return to FiveWin para Harbour/xHarbour
Who is online
Users browsing this forum: Google [Bot] and 59 guests
